博星优配【华安证券·债券研究】点评报告：稳定币与美债的逻辑关系——海外宏观研究笔记

（转自：华安证券研究）

什么是稳定币，稳定币的运行机制有何特点？

稳定币是一种以特定资产（如法币、商品或加密资产）为价值锚定物的加密货币，旨在维持币值相对稳定（通常与美元1:1挂钩）。由于比特币波动高、交易效率低，更适合作为“数字黄金”进行价值存储，而非作为日常支付工具。为填补比特币支付缺陷，2014年Tether发行首个主流稳定币USDT，标志着稳定币的诞生。其后 DeFi需求驱动了稳定币的增长扩张，在经历2022年算法稳定币UST崩盘、2023年硅谷银行爆雷致USDC短暂脱锚后，美国启动《稳定币法案》讨论，监管开始介入。目前稳定币总市值突破 2500亿美元，美元稳定币占比九成左右。

从运行机制来看，稳定币并非独立货币，而是链上法币凭证。将美元、美债等现实资产代币化，实现“链上映射”。稳定币通过智能合约将法币或美债资产转化为链上代币，实现“1:1锚定”，稳定币的核心是“凭证化”而非“货币化”。另外，法币抵押型稳定币（如USDT、USDC）由中心化机构（如Tether、Circle）发行，具备高度中心化特征。虽然DAI、LUSD等加密资产抵押型稳定币实现了部分去中心化，但稳定币在设计上即面临价格稳定性、去中心化、资本效率的不可能三角，算法稳定币尝试了去中心化设计但稳定性变差，UST曾因死亡螺旋机制崩溃。故稳定币和传统虚拟币的去中心节点有本质区别，而虚拟币的货币价值本质是去中心化，这就决定了稳定币注定无法成为“比特币”，它的价值只能来源于其它方面，即为美元、美债等现实资产在链上提供增量的支付服务价值。而这也使得，稳定币与美元、美债等锚定资产在价值核心上深度绑定。

稳定币和锚定资产虽按1:1挂钩发行，但转换过程具备非对称性，具备扩充锚定资产流通盘子的功能。细看从法币到稳定币的转换过程，用户在稳定币发行商平台存入一单位法币，对应发行商在链上铸造等值的稳定币，而返还稳定币时，法币划转回用户账户，回收的稳定币进行销毁。但无论是稳定币的铸造还是销毁，对应到法币，仅是在不同的银行账户间转换，并非冻结，法币仍通过发行方银行账户正常参与投资和流通。总结来说，当稳定币供应量不断增长时，对应锚定的法币并未从世界上“暂停流通”，而仅仅是换了一个银行账户继续活跃在投资市场上。一方面，创造了信用扩张，另一方面，由于目前发行方存储锚定法币的储备账户主要投向美债，故稳定币的增长，直接对应了美债配置力量的增长。

宏观视角下，稳定币将对美债产生怎样的影响？

稳定币为美元进行功能增益，扩张和强化美元需求，短期支撑汇率坚挺，美债受益。在扩张前期，“美元+稳定币”组合的链上交易优势或增加美元需求，但随着稳定币多样化，美元相对其它币种的链上结算优势可能消退，长期风险或将逐渐暴露。财政赤字货币化与稳定币规模膨胀可能透支信用，诱发汇率贬值。

但在长期，稳定币面临影子银行系统风险与杠杆风险扩大的问题。稳定币与美元的非对称化转换，实质是实现了“法币流动性增强”与“稳定币增量发行”的双轨扩张。货币总量来看，不增加M0，但扩张M2。私营机构掌控万亿级“影子货币”发行权仍有一定程度上的不可控风险。当规模突破临界点时，或可能将美国主权信用风险指数级放大至链上全球金融体系。此外，还面临杠杆效应对风险的进一步放大。对于稳定币发行商，100美元储备金购买美债后，美债可抵押融资再投资，形成链下再杠杆，Tether用美债回购协议加杠杆。而链上也会出现叠加效应：稳定币流入DeFi后，可通过借贷协议反复质押，进一步放大信用规模。

稳定币和美债的动态平衡在长期仍有脆弱性，稳定币的长期风险或将传导至美债，放大美债的风险波动，或将成为美债定价体系中，一项长期固定的风险来源项。美债与稳定币形成的“共生关系”导致了，一旦美债评级下调或出现违约预期，可能触发稳定币大规模脱锚。而反向来看，稳定币的挤兑也会引发美债的抛售，若稳定币遭遇信任危机，如脱锚事件，发行商需抛售美债兑付，推升短端收益率，形成“赎回→抛售→收益率飙升→进一步赎回”的螺旋。

微观视角下，各类稳定币具体如何支撑美债？

具体来看，稳定币分为支付型稳定币（非生息型）和收益型稳定币（生息型）两大类。支付型稳定币代表项目分别为USDT（1567亿美元）、USDC（618亿美元），两者合计占市场95%以上份额。收益型稳定币代表项目分别为Delta中性对冲型的Ethena USD、DeFi借贷型的Sky USD、RWA支持型的Ondo USD、混合收益型的Usual USD0++。

支付型稳定币体量超过95%，且储备资产购买美债的比例高于60%。USDT在2025年5月的美债持仓规模接近1200亿美元，占储备资产比例约在80%左右，USDC在2025年6月的美债持仓规模约为500亿美元左右，占储备资产比例约为80%左右。

支付型稳定币规模占据市场主导地位的原因，除了其简单易用的支付优势，还与其作为收益衍生品底层资产的潜在需求密切相关。用户可将USDC存入Coinbase Wallet生成sUSDC，或通过交易所质押USDT获得sUSDT，实现年化约4%-125%的收益。故支付型稳定币的一部分持有量也来源于其衍生品的“隐性价值”，且此部分占比具备一定规模，以真实收益型稳定币SyrupUSDC为例，其底层完全锚定USDC储备，市值达7.92亿美元，在收益型稳定币中位列第三。

机构用户亦可通过抵押美债而非法币的方式获得稳定币，其通过赋能美债的链上交易属性来在用户端创造增量美债需求的增长，但本身亦包含一部分存量美债配置资金。机构用户可通过两种方式实现美债抵押发行稳定币：1）直接抵押：机构将持有的美国国债存入银行或信托等合规托管机构，并以此发行1:1锚定的稳定币。2）间接质押：通过DeFi协议将美债代币化，生成稳定币。直接抵押案例如京东JDH稳定币，其通过合规托管机构存入美债，发行1:1锚定的稳定币，且用户保留美债所有权。间接质押案例如MakerDAO，支持将美国国债等现实世界资产作为抵押品，用户存入美债后通过智能合约生成 DAI。对机构客户而言，可通过美债抵押生成稳定币，无需出售美债即可获得流动性，用于其他投资或支付需求，故能够吸引传统金融机构使用。同时也为《GENIUS法案》下“非付息型稳定币”提供可能可行的模式：1）其符合条款“储备资产必须与发行方运营资金隔离，禁止再抵押”；2）由于其收益权本身归属客户，不涉及发行平台代为投资，并向用户分配收益，故若收益不来自稳定币本身，而是通过其他协议分配，如用户通过DeFi协议质押美债获得收益，或发行方以非稳定币形式返还美债利息，则可能不违反“稳定币不是投资合同，发行方可通过储备资产获利（如美债利息），但不可向用户付息”的禁令。3）虽然法案要求储备资产所有权必须归属发行方，但DAI、FRAX等去中心化稳定币不受直接约束，若用户通过DAO或智能合约发行抵押型稳定币，且不涉及“许可发行方”，则资产所有权可保留在用户钱包。故此渠道或成为未来稳定币一大稳定增长点，若实际落地验证合规性，未来也能稳定支持美债需求。

收益型稳定币规模少于5%，但未来具备增长潜力。RWA型目前美债配置比例在80%-100%、DeFi策略型美债配置比例在0%-10%，混合型美债配置比例在30%-50%。据估算，收益型稳定币的美债持仓约为66亿美元。未来对美债需求看，主流机构预测2030年稳定币约达 1.4-3.7万亿美元，对美债持将或增至1.2亿-2万亿美元。

总量来看，主流金融机构对稳定币的未来增长持乐观态度，并普遍预期其将成为美债市场的重要配置力量。2025年所有种类稳定币持有美债突破1200亿美元，成为美债第18大持有方。未来对美债需求看，主流机构预测2030年稳定币可达 3.5-5万亿美元，年增长率15%-25%，对美债持仓从当前2000-3000亿美元增至8000亿-1.5万亿美元，占比提升至20%-40%。其中摩根大通的预测偏保守，预测结果聚焦在 “付息禁令+流动性短板” 的短期制约，而渣打预测结果则极度乐观，强调 “监管开放+技术整合” 的长期红利。机构预测主要的分歧点在于对监管和传统金融机构参与度的预期。

GENIUS法案预计将如何影响稳定币对美债的支撑？

法案“投向限制为美元资产”+“禁止向客户付息”的组合，着力确保稳定币的增长量精准对应美债配置端的净增长。稳定币发行过程中，从法币向发行方账户移入的角度看，法案要求稳定币发行商必须持有100%高流动性美元资产作为储备，明确禁止非美元资产，高流动性美元资产具体包含美元现金、剩余期限不超过93天的短期美国国债、银行存款。尽管法案禁止向用户付息，但并未禁止发行方通过储备资产获取收益，发行方持有的短期美国国债或存款利息收入仍可归发行方所有。但由于银行将稳定币发行方视为高风险客户，常采取限制存款额度等措施，且法案允许的银行存款必须是FDIC受保存款，保险额度限制也迫使发行方只能将极小比例配置存款。另外，“储备资产不得用于质押融资、借贷、衍生品交易或任何高风险投资”的条款通过限制发行方其它收益来源的方式助推发行方追求收益的需求，在有限的资产选择下，出于维持运营的目的，发行方或不得不选择配置短期美国国债为主。另一方面，从法币从个人账户移出的角度看，立法者认为，付息可能诱导储户将资金从传统银行转移至风险更高的加密账户，削弱银行信贷功能并引发系统性风险。且稳定币的无息化亦削弱了其作为配置资产相对美债的竞争力，能够避免虹吸美债的配置资金。

同时，“禁止付息”也限制了稳定币的“影子银行”风险，避免拖累美债崩盘。法案的“禁止付息”也是出于防止其演变为“影子银行”的目的，防止其规避存款保险与银行资本充足率监管，通过利率竞争引发系统性风险。

但是，生息被打击亦可能影响稳定币原本的增长曲线：

USDT由于其投向票据等资产，不能满足“储备资产不得用于质押融资、借贷、衍生品交易或任何高风险投资。”的法案要求，面临退出美国市场或重组压力。而USDT作为目前市占率最高的稳定币，或对稳定币对美债的配置力有下滑影响。

虽另一大支付型稳定币巨头——USDC符合法案要求，但由于其衍生品sUSDC因付息机制和衍生品结构完全不符合支付稳定币的法案要求，面临全球合规围剿。故sUSDC贡献的、出于投资目的而持有USDC的份额将出现下滑，拖累USDC本币的总量。

收益型稳定币不在法案合规范围内，虽然目前规模不足5%，影响力有限。但收益型稳定币未来增长潜力巨大，是构筑未来稳定币总量增长的重要组成部分，若去除收益型稳定币，则目前针对稳定币的未来增长模型或要重新计算。

另外，稳定币的监管化转变亦或导致当前部分稳定币的存量需求收缩。原本“挖矿→获得比特币→兑换成稳定币→兑换成美元”的模式是基于稳定币的弱监管性产生的一类稳定币需求线。该条线由于隐匿性导致难以测算其具体贡献的稳定币需求量级，稳定币监管化转变对此部分需求的冲击具有不确定性。

故基于以上法案影响，未来稳定币增长趋势可以从两方面来看：

一方面，乐观情境下监管对生息型稳定币实际监管力或有限，多数品种稳定币合规化可能会比较顺利。

法案的实际监管效力或低于预期。链上生息稳定币的生存空间或从公开转向地下。一方面，完全去中心化协议的“监管免疫”技术层面无法禁止，智能合约一旦部署便不可篡改。监管或仅能警示“非合规产品无保护”，但无法阻止用户通过VPN自托管钱包参与。

多数品种稳定币或能够实现合规化转型，继续保持增长趋势。USDC的衍生品 sUSDC或可通过此方式转型为证券化产品，将收益权拆分为证券型代币，接受SEC注册监管，用户通过持有代币获取美债利息。sUSDT或可通过退守离岸市场改造为“非生息质押凭证”。USDT等原生代币或可通过放弃付息功能实现合规，用户通过合规DeFi协议质押获取收益，实现收益与支付分离。对于收益型稳定币，高盛、富达等资管巨头可能发行代币化货币市场基金，替代现有DeFi收益协议。

另一方面，悲观情景为生息型稳定币被打击、且支付型稳定币规模增长受限。稳定币巨头USDT的合规转型或仍要时间，因为触及了根本商业模式的变更，不再能通过长期美债套利、高风险资产投资获益。

综合考虑各类因素，我们的观点是：1）短期来看，法案落地后，出于市场对所持稳定币品种或不能满足合规的预期，或带来抛售风险，利空稳定币的短期增长。2）中期来看，各品种稳定币或陆续实现合规化转型，且受益于行业在监管下更规范，将有更多大型机构参与进一步支撑稳定币市场。鉴于USDC、USDT作为头部支付型稳定币已成为短期美债的关键增量买家，且实际市场风险可控，故《GENIUS法案》将优先保障此类‘功能纯粹型’项目的合规路径，或为其提供合规缓冲，根据实际受冲击情况，针对其相关衍生品的合规细则或也有调整完善的空间。3）长期来看，稳定币与法币的双轨扩张格局仍有隐忧，需要严格限制在和全球经济增速相匹配的区间中，作为系统性风险源将长期被市场关注。

对于美债的影响而言，稳定币规模增长的风险在长端，长期限美债或在风险担忧中承压。而对于短期限美债，底层逻辑为稳定币的或有爆雷风险长于短端美债的期限，故对短端影响有限。短期限美债的短期风险或来源于法案落地导致稳定币业态短期内产生结构性震荡，可能会有扰动和抛压，但后续随着市场环境重新企稳，市场恐慌情绪逐步消化及稳定币发行方完成储备资产调仓后，短期限美债仍有回弹利好。

“

风险提示

监管效力不确定性风险、国际局势不确定性风险。

]article_adlist-->

引言

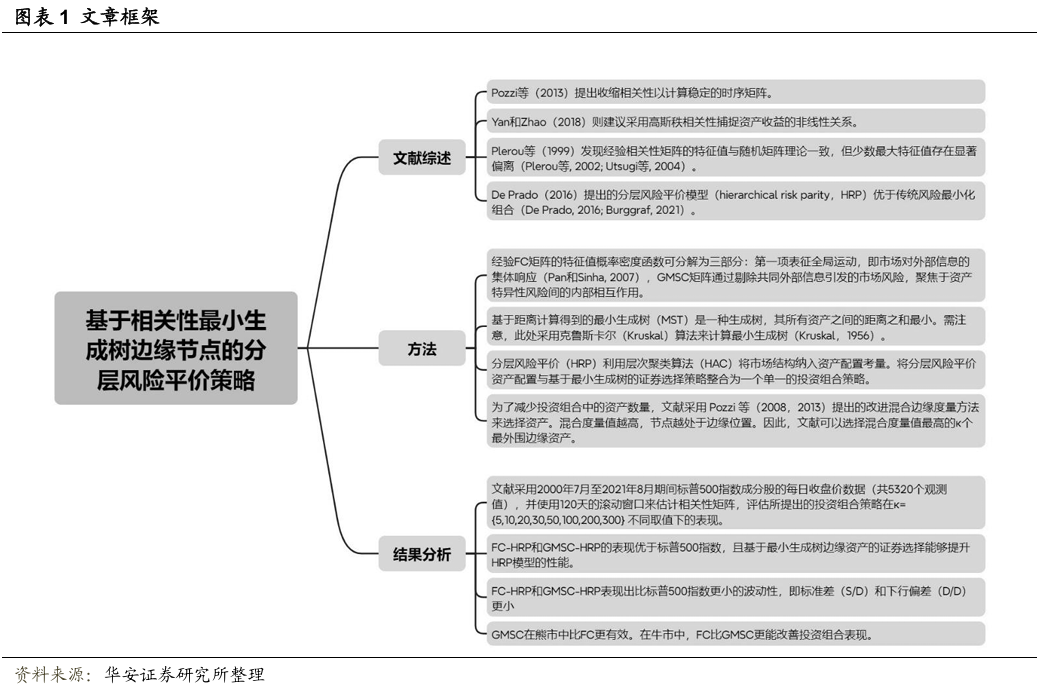
金融市场的动态变化受到各类内外因素的影响，这种特性使得金融市场常被建模为复杂系统（见Mantegna, 1999; Tumminello等, 2005）。具体而言，基于相关性的金融网络主要通过最小生成树（MST）和平面极大过滤图（如Aste等, 2010; Di Matteo等, 2010）进行研究，应用于风险管理与投资组合优化领域（Mastromatteo等, 2012; Wang等, 2017）。其中，金融网络中边缘节点对构建稳健投资组合的重要性已被发现（Onnela等, 2003; Pozzi等, 2013），但既有研究仅考虑了均值-方差资产配置策略。

相关性矩阵的可靠性依赖统计估计方法。例如Pozzi等（2013）提出收缩相关性以计算稳定的时序矩阵，而Yan和Zhao（2018）则建议采用高斯秩相关性捕捉资产收益的非线性关系。另一种思路是从矩阵中提取显著相互作用：Plerou等（1999）发现经验相关性矩阵的特征值与随机矩阵理论一致，但少数最大特征值存在显著偏离（Plerou等, 2002; Utsugi等, 2004），这些最大特征值被视为代表金融网络核心动态的全局运动（Marcenko和Pastur, 1967; Jiang等, 2014）。基于Song等（2016）和Borghesi等（2007）的研究，文献提出通过从全互相关矩阵（full cross-correlation）中减去全局运动（global motion）来构建新型相关性矩阵。

从马科维茨模型（Markowitz, 1968）到风险平价策略（Qian, 2011），传统组合构建过程缺乏金融市场的层次结构。对此，De Prado（2016）提出的分层风险平价模型（hierarchical risk parity，HRP）优于传统风险最小化组合（De Prado, 2016; Burggraf, 2021）。但HRP要求完整的市场层次结构，对海量投资管理造成负担。为突破此限制，文献提出基于相关性MST边缘节点池的资产选择HRP模型，采用全互相关（full cross-correlation，FC）和全局运动调整相关性（global motion subtracted correlation，GMSC）两种矩阵。实证表明，这两种矩阵均能保持或提升组合表现，但随选定资产数量与市场条件呈现差异化特征。

方法

2.1 相关性矩阵与全局运动

2.2 基于最小生成树边缘节点的分层风险平价

可以利用距离度量 D 将相关矩阵映射到一个度量空间，其中距离度量 D 的表达式为：

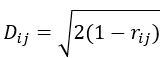
这里r_ij是完全互相关矩阵（FC）或减去全局运动后的相关矩阵（GMSC）中的元素。基于距离计算得到的最小生成树（MST）是一种生成树，其所有资产之间的距离之和最小。需注意，此处采用克鲁斯卡尔（Kruskal）算法来计算最小生成树（Kruskal，1956）。

分层风险平价（HRP）利用层次聚类算法（HAC）将市场结构纳入资产配置考量。有趣的是，采用单链接准则的最小生成树与层次聚类算法在本质上是相同的（Mantegna 和 Stanley，1999；Marti 等，2021），该算法的具体描述见图表2（Müllner，2011；Berthold 和 Höppner，2016）。因此，可将分层风险平价资产配置与基于最小生成树的证券选择策略整合为一个单一的投资组合策略。由于用于生成最小生成树的完全互相关矩阵和减去全局运动后的相关矩阵会随时间变化，本研究提出的投资组合策略在每次再平衡时都会重新纳入金融市场的新层次结构。

在完成层次聚类算法的树状聚类后，会进行准对角化处理。将未标准化的对数收益率协方差矩阵重新排列，使相似资产彼此靠近，而相异资产彼此远离。单链接层次聚类算法会生成一个 (N−1)×4 的矩阵，其中链接矩阵的每一行可能包含聚类或构成元素。从矩阵的最后一行开始，递归地将行中的聚类替换为其构成元素，直到没有聚类剩余为止。最后，根据单链接层次聚类值的顺序对原始协方差矩阵的行和列进行排序。

随后，利用 De Prado（2016）提出的递归二分法来计算投资组合权重，具体描述见图表3。具体而言，递归二分法从最终的聚类开始。注意，所有资产的初始权重均设为 1。通过向下遍历树结构，将包含所有资产的聚类拆分为两个子聚类。拆分过程会按比例将上层聚类的投资列表分为两个列表。然后，计算每个聚类的方差，作为每个子聚类逆方差分配投资组合的方差。根据每个聚合方差，计算拆分因子，并利用该因子重新调整每个子集的资产配置比例。

为了减少投资组合中的资产数量，文献采用 Pozzi 等（2008，2013）提出的改进混合边缘度量方法来选择资产。混合度量值越高，节点越处于边缘位置。因此，文献可以选择混合度量值最高的κ个最外围边缘资产。

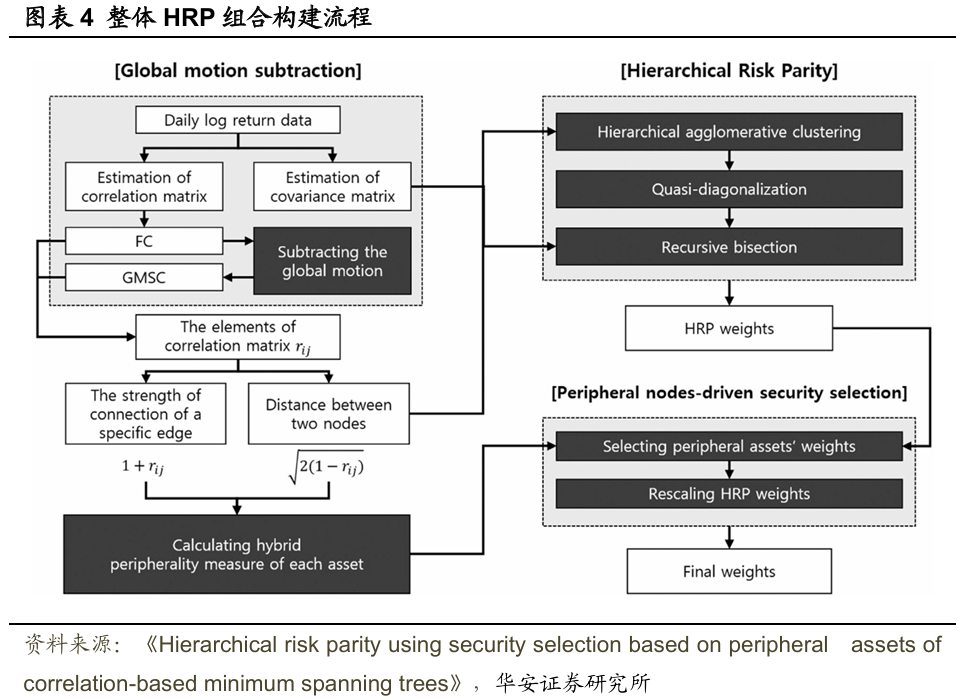
投资组合管理的最后一步是对所选资产的分层风险平价权重进行重新调整。目标是生成最终保持金融市场整个层次结构特征的分层风险平价权重。因此，将每个所选资产的权重除以所有所选资产权重的总和。最后，使用证券选择策略为完全互相关矩阵和减去全局运动后的相关矩阵构建分层风险平价投资组合，整体流程可概括为图表4所示。

实证结果

3.1 数据与回测设置

文献采用2000年7月至2021年8月期间标普500指数成分股的每日收盘价数据（共5320个观测值），并使用120天的滚动窗口来估计相关性矩阵。因此，在每次再平衡时，文献仅考虑那些至少有120个对数收益率的资产。投资组合在每月的第一个交易日进行再平衡。因此，回测的第一天是2001年1月2日，并持续推进至2021年8月31日。标普500指数中的资产数量从2001年1月的497只开始，到2021年8月增至504只。文献评估了所提出的投资组合策略在κ={5,10,20,30,50,100,200,300} 不同取值下的表现，并将其与标普500指数以及使用全部资产的分层风险平价（HRP）策略的表现进行了对比。

3.2 相关矩阵与最小生成树

图表5展示了2021年8月1日完全互相关（FC）矩阵特征值的概率密度函数。部分FC矩阵的特征值显著超出了马尔琴科-帕斯图尔（Marchenko–Pastur）分布的上限。此外，蓝色条形图代表的是通过打乱各资产时间序列的对数收益率后估计得到的替代相关矩阵的特征值分布（Pan和Sinha，2007）。文献确认，替代相关矩阵的所有特征值均未超过随机矩阵特征值的理论上限。

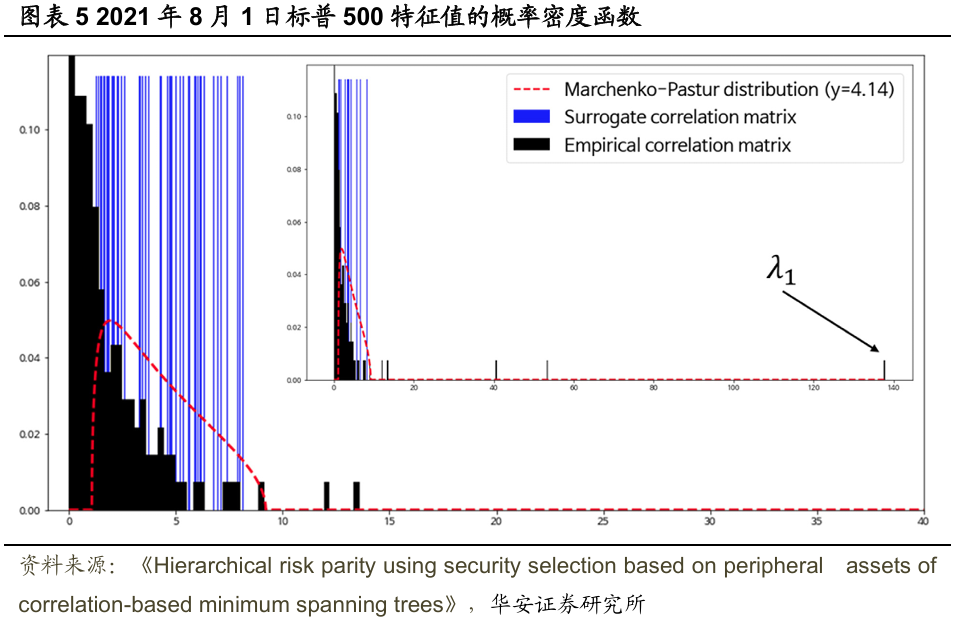
图表6展示了2021年8月1日的FC矩阵、全局运动相关（GMC）矩阵和减去全局运动后的相关（GMSC）矩阵。图3(a)中经过准对角化处理的FC矩阵显示，在对角线上有许多显著的簇（以蓝色方块表示）。图3(b)中的GMC矩阵揭示了全局运动情况，右上角显示的是引领市场的资产。图3(c)中的GMSC矩阵则显示出较少的簇和较低的相关性。因此，GMSC矩阵强调了那些收益率对市场条件变化不太敏感的资产的重要性。随后，文献对GMSC矩阵也进行了准对角化处理，结果如图3(d)所示。

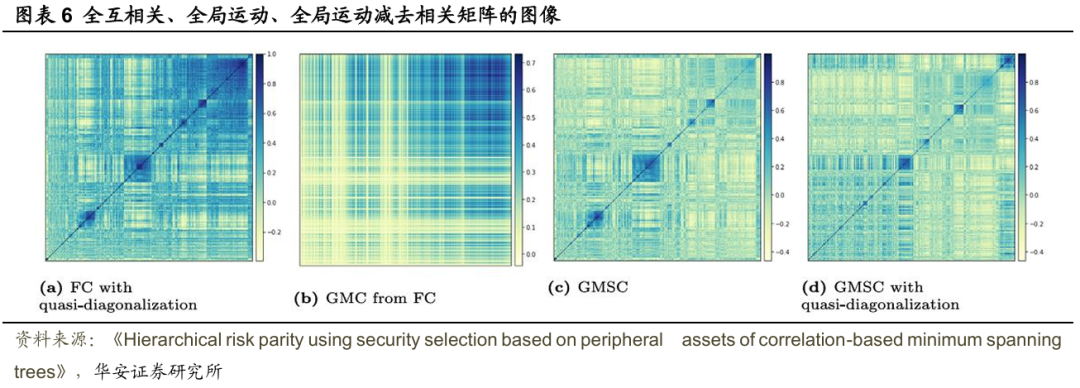
文献进一步利用图表7中的最小生成树（MST）样本配置来分析金融市场的结构以及所选边缘资产的情况。图表7的 (a)–(d)和(e)–(h)分别展示了2021年8月1日，对于10个、30个、50个和100个所选边缘资产，FC矩阵和GMSC矩阵的MST。

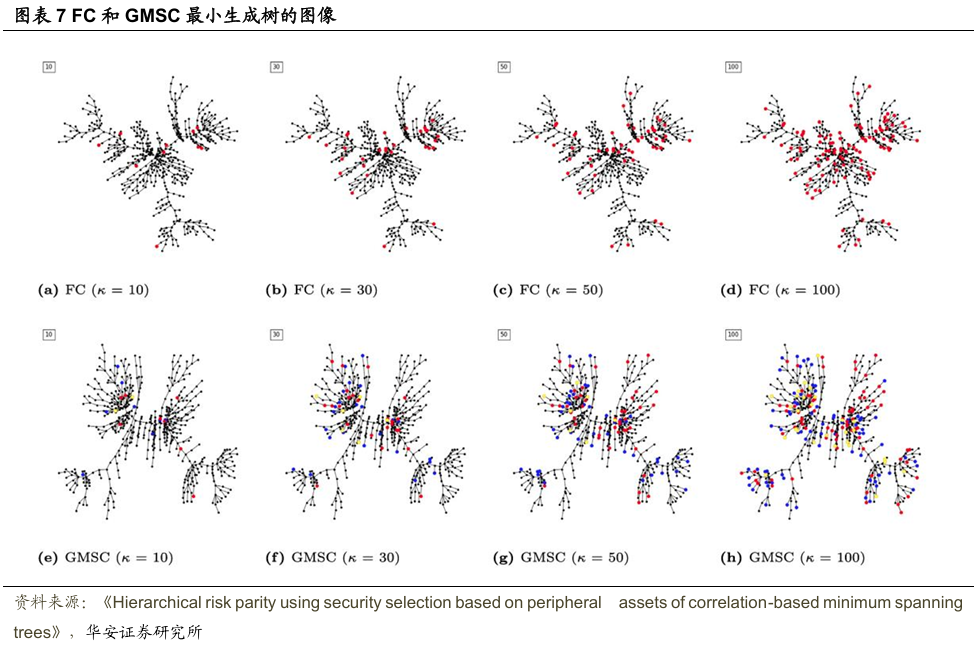
FC矩阵的MST呈现出辐射状的层次结构，其中连接度最高的资产位于中心。而GMSC矩阵的MST则相对分散，去除了最中心的资产（其价格动态预计会引领金融市场），从而提供了更为细分的层次结构。此外，对于不同的κ值，FC矩阵（红色）和GMSC矩阵（蓝色）中选出的所有边缘资产都远离MST的中心，且连接较少。同时被选中的资产数量较少（黄色）则表明了FC矩阵和GMSC矩阵在证券选择上的差异。

3.3 投资组合业绩

在回测期间，针对不同数量的资产（κ={5,10,20,30,50,100,200,300}），评估了基于完全互相关（FC）矩阵（FC-HRP）和减去全局运动后的相关（GMSC）矩阵（GMSC-HRP）的分层风险平价投资组合的表现，并与基准进行了对比。需注意，使用全部资产的FC-HRP是De Prado（2016）中提出的HRP模型。回测过程中考虑了10个基点的交易成本，并剔除了标普500指数中不再符合条件的资产。

首先，从图表8的累计投资组合对数收益率来看，除了使用较小κ值的GMSC-HRP外，FC-HRP和GMSC-HRP的表现均优于标普500指数。此外，使用全部资产的FC-HRP和GMSC-HRP并非累计对数收益率最高的投资组合，这表明所提出的证券选择方法是有效的。

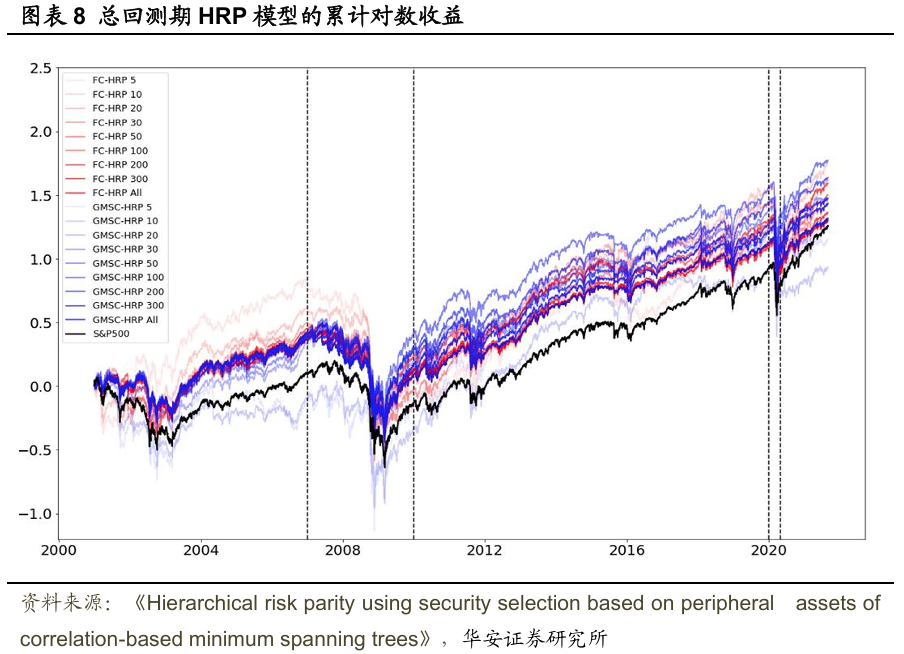
体而言，FC-HRP和GMSC-HRP的累计对数收益率趋势与标普500指数几乎相同。不过，随着κ值的减小，这种趋势的相似性逐渐减弱。即便趋势相似，FC-HRP和GMSC-HRP的投资组合表现仍高于基准，这表明采用证券选择的FC-HRP和GMSC-HRP是智能贝塔策略，它们利用金融市场结构中的边缘资产作为因子，旨在提高收益并降低风险。

图表9详细总结了投资组合的表现。在所有资产都被选中的情况下，FC-HRP和GMSC-HRP在大多数业绩指标上均优于标普500指数。除了使用5种资产的情况外，使用证券选择的FC-HRP在所有κ值下均获得了比使用全部资产更高的年化复合收益率（C/R）。

类似地，除了使用5种和10种资产的情况外，使用证券选择的GMSC-HRP在所有κ值下均产生了比使用全部资产和标普500指数更高的C/R。尽管资产数量分别减少到了100种和200种，但FC-HRP和GMSC-HRP仍表现出比标普500指数更小的波动性，即标准差（S/D）和下行偏差（D/D）更小。在50≤κ≤300的范围内，FC-HRP以及κ=50,200,300时的GMSC-HRP显示出比使用全部资产更小的最大回撤（MDD）。

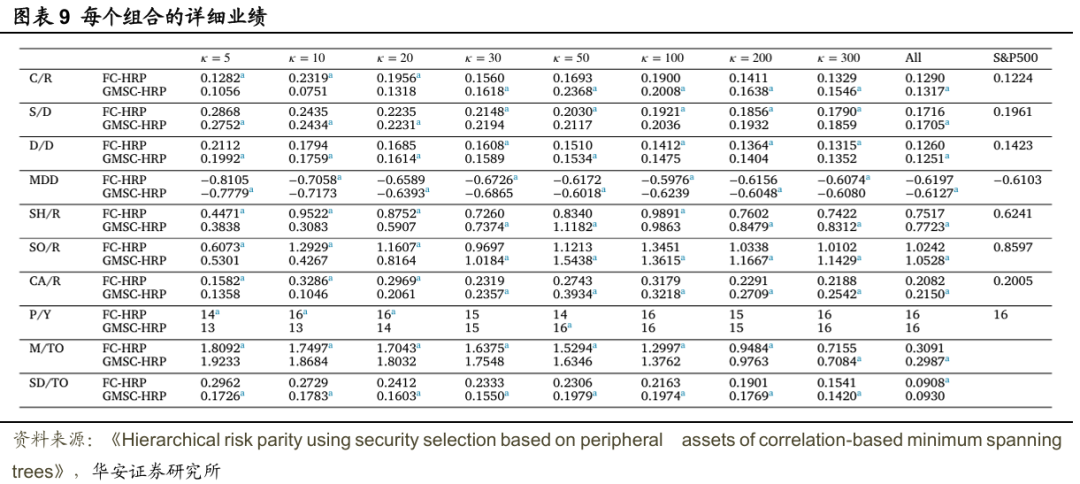
有趣的是，采用证券选择的FC-HRP和GMSC-HRP在比使用全部资产和标普500指数时表现出更高的收益和相当的波动性。这一推断得到了风险调整后收益指标的支持：夏普比率（SH/R）、索提诺比率（SO/R）和卡尔马比率（CA/R）。从SH/R和SO/R的角度来看，κ=50时的GMSC-HRP是最优策略。大多数采用证券选择的FC-HRP和GMSC-HRP在SH/R和SO/R上均高于使用全部资产和标普500指数的情况。对于CA/R，除了κ=5的情况外，FC-HRP在所有κ值下均优于基准；而GMSC-HRP在30≤κ≤300和20≤κ≤300的范围内分别优于使用全部资产和标普500指数的情况。因此，FC-HRP和GMSC-HRP的表现优于标普500指数，且基于最小生成树边缘资产的证券选择能够提升HRP模型的性能。

此外，文献在证券选择方面对FC-HRP和GMSC-HRP进行了比较。首先，在κ=5,10,20的情况下，FC-HRP在年化复合收益率（C/R）、风险调整后收益和盈利年份（P/Y）方面均优于GMSC-HRP。然而，GMSC-HRP在标准差（S/D）、下行偏差（D/D）和最大回撤（MDD）方面表现出更低的风险。当30≤κ≤300时，GMSC-HRP在C/R和风险调整后收益方面优于FC-HRP，但两者的盈利年份（P/Y）和最大回撤（MDD）相当。

月度换手率均值（M/TO）和标准差（SD/TO）按照Gu等人（2020）所述的方法进行计算。如果投资组合中的所有资产在再平衡时都被替换，则M/TO的值为2；如果没有资产被替换，则值为0。需要注意的是，较高的换手率意味着较高的交易成本。FC-HRP的M/TO较小，但GMSC-HRP的SD/TO较小。

综上所述，FC-HRP适合资本有限且资产数量适中的个人投资者，而GMSC-HRP则适合考虑大规模资本和丰富资产进行投资组合管理的机构投资者。

文献还进一步研究了不同子时期的投资组合表现，这些子期间包括几个牛市、震荡市和熊市。整个研究期间被划分为五个子时期：2001年1月至2006年12月的震荡市、2007年1月至2009年12月的次贷危机、2010年1月至2019年12月的危机后长期牛市、2020年1月至2020年4月的COVID-19疫情危机，以及2020年5月至2021年8月的疫情后牛市。投资组合表现总结在图表10中。

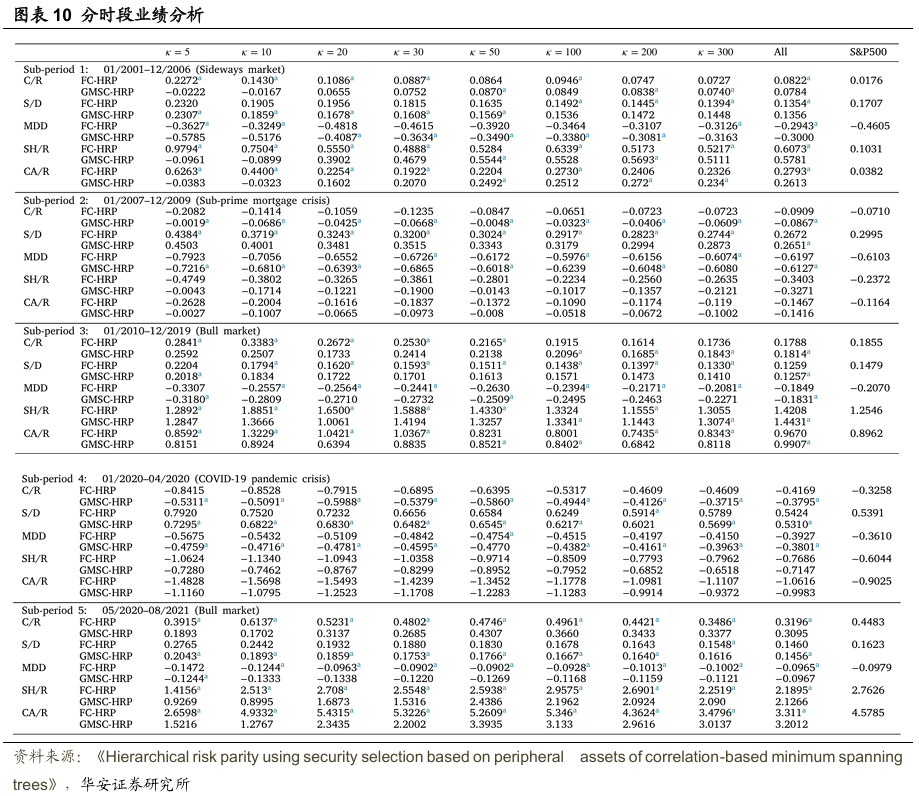
在第一个子时期（震荡市），使用全部资产的两个投资组合在所有绩效指标上均优于标普500指数。即使资产数量减少到50种，两个投资组合的表现也高于标普500指数。这表明基于最小生成树边缘资产的证券选择在震荡市中是有效的。特别是，5≤κ≤100时的FC-HRP和κ=50,100,200时的GMSC-HRP记录了比使用全部资产的各自HRP更高的C/R。当50≤κ≤300时，两个投资组合的风险均低于标普500指数。对于大多数κ值，FC-HRP的夏普比率（SH/R）高于使用全部资产和标普500指数的情况，而GMSC-HRP则未能超越使用全部资产的情况。具体来说，当κ≤30时，FC-HRP优于GMSC-HRP，这与整个研究期间的表现一致。

在第二个子时期（次贷危机），使用全部资产的FC-HRP和GMSC-HRP均未能超越标普500指数。然而，采用证券选择的两个投资组合在投资组合风险方面均优于标普500指数。对于C/R，GMSC-HRP在所有κ值下均优于标普500指数，而FC-HRP仅在κ=100时优于标普500指数。本质上，所提出的证券选择在次贷危机期间改善了投资组合表现，其中基于GMSC的最小生成树表现出比FC更高的性能。

在第三个子时期（金融危机后的牛市），使用全部资产的两个投资组合在所有绩效指标上均优于标普500指数，除了C/R方面，而采用证券选择的两个投资组合甚至在C/R方面也优于标普500指数。此外，在风险相对较低的情况下，对于大多数κ值，FC-HRP和GMSC-HRP在SH/R方面均优于标普500指数。与使用全部资产相比，具有较小κ值的两个投资组合在SH/R和卡尔马比率（CA/R）方面均有所改善。特别是，κ=20时的FC-HRP的SH/R显著高于两个基准。综上所述，在牛市中，基于FC-HRP的证券选择比基于GMSC-HRP的证券选择更有效，且在较低的κ值下可以预期更好的表现。

在第四个子时期（COVID-19疫情危机期间的熊市），使用全部资产和采用证券选择的两个投资组合在所有绩效指标上均未能超越标普500指数。在C/R和MDD方面，GMSC-HRP在所有κ值下均优于FC-HRP。此外，除了κ=200外，GMSC-HRP的S/D在所有κ值下均小于FC-HRP。与第二个子期间一样，GMSC在熊市中比FC更有效。

在最后一个子时期（疫情后牛市），使用全部资产的两个投资组合在S/D和MDD方面均低于标普500指数。κ=10,20,30,50,100时的FC-HRP同时显示出比标普500指数和使用全部资产更高的C/R。GMSC-HRP的C/R低于标普500指数，但对于κ=20,50,100,200,300的证券选择则改善了C/R。此外，在较小的κ值下，FC-HRP在SH/R和CA/R方面显著优于两个基准。综上所述，通过证券选择，两个投资组合均实现了比使用全部资产更好的表现。此外，与第三个子期间的结果一致，在牛市中，FC比GMSC更能改善投资组合表现。

结论

文献提出了基于两种不同相关矩阵（完全互相关矩阵FC和减去全局运动后的相关矩阵GMSC）的最小生成树驱动证券选择方法的分层风险平价（HRP）模型。即便所选资产数量减少，所提出的投资组合仍能超越基准，这表明了边缘资产选择方法的有效性。此外，文献发现，在危机后的牛市中，选择较少资产的FC-HRP在弥补投资组合损失方面表现更优；而在金融危机期间，选择较多资产的GMSC-HRP则能够最小化投资组合损失。因此，文献预计所提出的HRP模型在实际投资组合管理中将对个人投资者和机构投资者大有裨益。

文献来源：

核心内容摘选自Younghwan Cho, Jae Wook Song在Finance Research Letters上的论文《Hierarchical risk parity using security selection based on peripheral assets of correlation-based minimum spanning trees》。

“

风险提示

]article_adlist-->

（1）宏观环境风险。公司的主营业务为软床、床垫、沙发等软体家具及配套家居产品的研发、设计、生产和销售，产品定位中高端，属耐用消费品。公司产品的市场销售受经济形势和宏观调控、房地产市场景气度、居民可支配收入、消费理念及消费水平等因素的影响较大。如果全球经济出现重大波动，国内外宏观经济或消费需求增长不及预期，消费降级趋势延续，房地产行业持续下行，则公司所处的软体家具行业市场增长也将随之减速，从而对公司产品销售造成影响。若公司不能采取有效措施应对，公司经营可能面临业绩波动的风险。

（2）主要原材料价格波动风险。公司直接材料占主营业务成本的比例为 54.68%，占比较高，其中主要原材料为面料、海绵、皮料、钢线、乳胶和 3D 棉等，占原材料的 60%左右。上述主要原材料的价格受其行业竞争状况、国际贸易往来、供需变化等多方面因素影响。若未来以上因素发生变化，相关主要原材料市场价格存在大幅波动的可能，如果公司不能采取有效应对措施，公司的经营业绩将受到不利影响。

（3）市场竞争加剧风险。随着健康睡眠理念不断深入人心，国内消费者对中、高端软床产品的接受程度越来越高，吸引国内外众多竞争对手加大对软床市场的投入和布局，市场竞争程度有所加剧。若公司在未来的市场竞争过程中，不能有效保持品牌及服务美誉度、不能持续保持产品竞争力及产品质量优势、不能持续获取主流KA商场门店区位优势、不能有效构建电商平台、社交媒体、直播销售等线上销售渠道等，将削弱公司的市场占有率，或将对公司的经营业绩的增长造成不利影响。

（4）品牌运营与管理风险。作为国内知名的床垫品牌之一，“慕思”产品设计、质量和售后服务获得了众多消费者的认同。虽然公司较高的品牌知名度可以提升产品附加值，但品牌知名度的建立和维护需要持续较高成本的投入和可靠的产品质量作为支撑，随着公司经营规模不断扩大，品牌运营与管理的工作难度日益增加，公司可能存在因品牌宣传推广定位偏差、品牌代言人行为失当等引起负面报道，以及宣传文案表述不当而引发品牌舆情等风险。同时，公司所在行业内存在不规范使用商标、碰瓷知名商标等损害诚信经营企业正当利益的情形，公司产品或商标等知识产权存在被恶意竞争对手模仿甚至仿冒可能，该等仿冒伪劣产品将严重冲击消费者对公司产品质量的信赖或将带来潜在知识产权纠纷。上述风险因素可能直接影响公司的品牌形象和品牌美誉度，进而对公司经营带来不利影响。

（5）经销商管理风险。经销及其专卖店模式是公司最主要的销售方式。经销商专卖店销售模式有利于公司借助经销商的区域资源优势拓展营销网络与服务网络，为消费者提供更好的产品体验，并对各级市场进行有效渗透、提高产品的市场占有率，截至2024年末，公司通过经销渠道开拓线下专卖店约 5,400 个。公司由于经销商及其门店数量众多，地域分布较为分散，客观上增加了公司对经销商及其门店的管理难度。若个别经销商未按照公司经销商管理办法及经销协议约定进行销售、业务宣传、品牌管理，则将可能对公司的品牌和声誉带来不利影响。

“

重要提示

本报告摘自华安证券2025年7月2日已发布的《稳定币与美债的逻辑关系——海外宏观研究笔记（二）》，具体分析内容请详见报告。若因对报告的摘编等产生歧义，应以报告发布当日的完整内容为准。

“

分析师介绍

分析师：颜子琦执业证书号：S0010522030002

分析师：洪子彦执业证书号：S0010123060036